钢混组合梁弹性设计方法应用

钢混组合梁弹性设计方法应用

一、简介

对于一般钢混凝土组合梁，规范给出的是塑性算法，塑性算法可以最大限度利用材料强度，其经济性是不言而喻的。关于弹性算法规范并未给出具体计算方法，但也大体给出了弹性计算原则，即采用换算截面法验算荷载效应设计值在组合梁截面产生的应力(包括正应力和剪应力等)小于材料的设计强度。弹性计算是当塑性算法不可用时，退而求其次的一种做法，使用场景主要有如下两种情况，其一为直接承受动力荷载；其二当受压板件宽厚比不满足塑性截面要求时。根据一般工程经验，钢混组合梁更多的应用于简支梁设计。

二、钢混组合梁弹性计算方法

1、换算截面

由于钢与混凝土两种材料性质不同，不能直接采用截面模量进行计算，按照弹性模量关系进行折算，为方便计算，将混凝土材料等效为钢材的原则进行换算，为保证混凝土截面形心不变，采用宽度等效，厚度不变，则换算截面宽度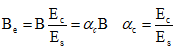

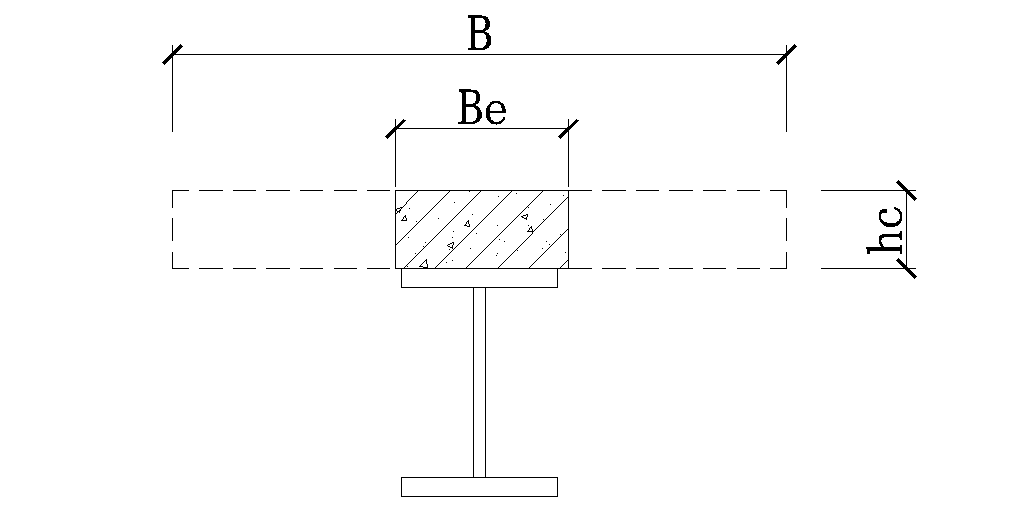
2、弹性算法简述

由于截面非对称，对于简支梁需要分别验算跨中上截面边缘压应力及下截面边缘拉应力是否满足强度要求，截面抗弯模量W1及W2根据材料力学相关公式进行计算，此处不再详赘述。中性轴及上下边缘应力计算式如下：

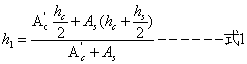
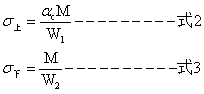
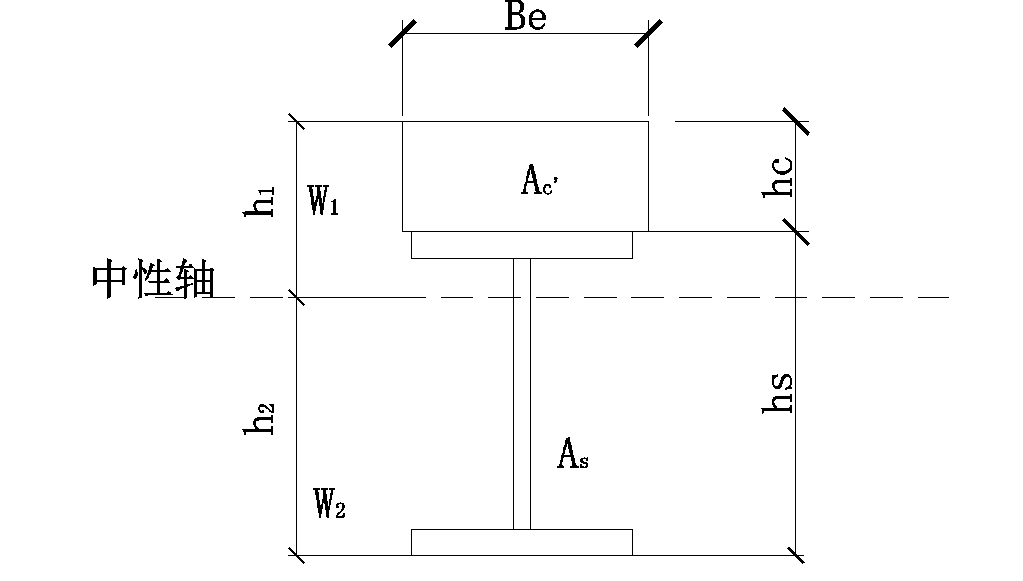
3、组合梁二阶段设计

当采用弹性计算方法时，根据规范要求，浇筑混凝土时钢梁下无支撑时，需要按两个受力阶段进行计算，第一阶段在混凝土翼板强度达到75％以前，组合梁的自重以及作用在其上的全部施工荷载由钢梁单独承受，此时按一般钢梁计算其强度、挠度和稳定性；第二阶段当混凝土翼板的强度达到75％以后，所增加的荷载全部由组合梁承受，在验算组合梁的挠度以及强度时，应将第一阶段和第二阶段计算所得的挠度或应力相叠加，作为钢梁最终应力；需要注意一点是，关于施工活荷载考虑其仅在第一阶段存在，施工完毕后此荷载已经不存在，故在进行二阶段叠加时可不叠加施工活荷载的作用。另外对于钢梁而言抗剪很少起控制，故以下主要针对抗弯强度验算进行分析计算，对于挠度计算不管是采用弹性算法还是塑性设计，挠度计算是完全一样的，即均采用弹性算法，规范有明确计算公式，此处不再赘述。

（1）第一阶段计算

第一阶段计算施工过程钢梁承载问题，荷载为钢梁及楼板自重，活载为施工活荷载；

弯矩基本组合：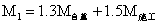   

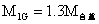
钢梁上下翼缘计算应力：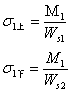

恒载下钢梁下翼缘计算应力：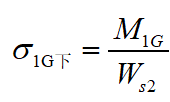

（2）第二阶段计算

第二阶段为平时工况下承载，荷载为附加恒载，即面层荷载及吊挂等荷载，活载为平时使用荷载；

弯矩基本组合：

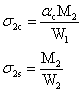则叠加第一阶段结果，钢梁下翼缘边缘最终应力为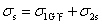，组合后钢梁上翼缘受力很小，二阶段可不作验算。

三、案例

某简支梁廊桥跨度20m，梁间距2.5m，混凝土板厚度100mm，附加面层荷载2.0kn/㎡，活荷载3.5kn/㎡，钢梁截面采用H1000x200（x300）x16x20，材质Q355B，复核该组合梁受力。

1、采用以上公式进行二阶段计算结果如下：

2、采用有限元软件进行对比计算

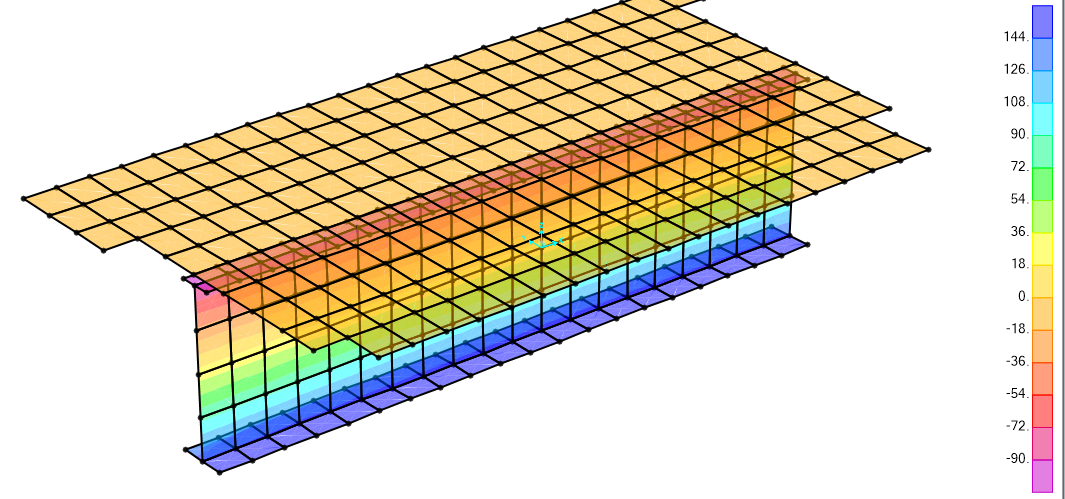
（1）砼板、钢梁板件均采用壳单元模拟，取2.5m宽标准单元，保证形心对齐，定义阶段施工工况进行模拟，第一阶段混凝土板不参与计算，截面内力采用截面切割提取。以下仅对比第一阶段恒载及第二阶段恒+活工况下结果。

截取跨中局部：

第一阶段结果（1.3D）：

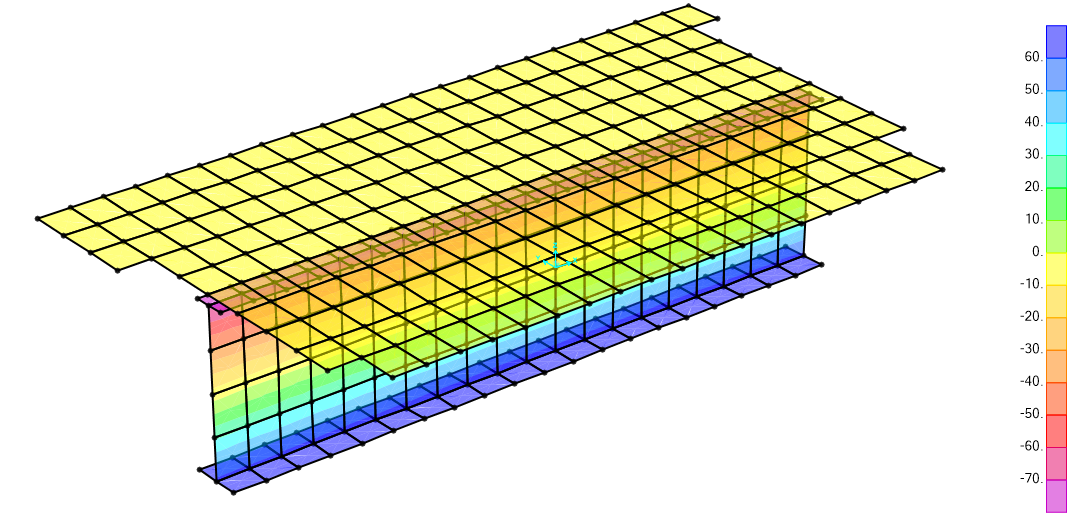
第二阶段结果（1.3D+1.5L）：

3、两种算法结果对比如下：

四、小结

1、对于组合梁弹性算法采用以上公式计算结果与有限元结果非常接近，说明按以上公式计算是合理的。

2、组合梁弹性算法由于涉及两阶段计算，过程相对繁琐，但由于考虑了混凝土受压翼缘作用，截面又可采用不对称截面，相对于纯钢梁而言钢材用量有较大程度节约；

3、当无法采用塑性算法时，可考虑采用。